Случай для изученного алгоритма сортировки

Сегодняшний выбор статей основывается на работе, проделанной в SageDB, и фокусируется на классической задаче информатики-сортировке. В наборе данных с 1 миллиардом элементов Learned Sort превосходит следующего лучшего конкурента, RadixSort, в 1,49 раза. Что действительно поразило меня, так это то, что этот результат включает в себя время, затраченное на обучение используемой модели!

Большая идея

Предположим, у вас есть модель, которая дает элемент данных из списка, может предсказать его положение в отсортированной версии этого списка. 0.239806? Это будет на позиции 287! Если бы модель имела 100% точность, она дала бы нам завершенную сортировку, просто пробежав по набору данных и поместив каждый элемент в его прогнозируемое положение. Но есть одна проблема. Модель со 100% точностью, по существу, должна видеть каждый элемент в полном наборе данных и запоминать его положение – нет никакого способа обучения, а затем использование такой модели может быть быстрее, чем просто сортировка, так как сортировка является частью ее обучения! Но, возможно, мы можем взять выборку подмножества данных и получить модель, которая является полезной аппроксимацией, изучив аппроксимацию к CDF (кумулятивной функции распределения).

Если мы можем быстро построить достаточно полезную версию такой модели (мы можем, мы обсудим, как это сделать позже), то мы можем сделать быструю сортировку, сначала сканируя список и помещая каждый элемент в его приблизительное положение, используя предсказания модели, а затем используя алгоритм сортировки, который хорошо работает с почти отсортированными массивами (Сортировка вставки), чтобы превратить почти отсортированный список в полностью отсортированный список. В этом суть Ученого Рода.

Первая попытка

Базовая версия Learned Sort-это неуместная сортировка, то есть она копирует отсортированные элементы в новый целевой массив. Он использует модель для прогнозирования слота в целевом массиве для каждого элемента в списке. Что должно произойти, если модель предсказывает (например) слот 287, но в целевом массиве в этом слоте уже есть запись? Это столкновение. Кандидатами на эти решения являются:

1. Линейное зондирование: сканируйте массив на наличие ближайшего свободного слота и поместите элемент туда
2. Цепочка: используйте список или цепочку элементов для каждой позиции
3. Ведро разлива: если слот назначения уже заполнен, просто поместите предмет в специальное ведро разлива. В конце прохода отсортируйте и объедините ведро разлива с целевым массивом.

Авторы экспериментировали со всеми тремя и обнаружили, что подход "ведро для разлива" работает для них лучше всего.

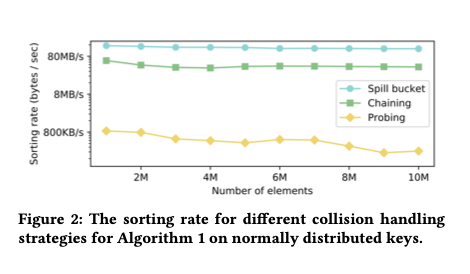
Результирующая производительность зависит от качества предсказаний модели, более качественная модель приводит к меньшему количеству коллизий и меньшему количеству неупорядоченных элементов, которые должны быть исправлены в конечном проходе сортировки вставки. Поскольку мы сейчас обсуждаем детали модели, интересный вопрос заключается в том, что происходит, когда вы даете этому ученому виду идеальный оракул с нулевыми накладными расходами в качестве модели? Скажем, мы хотим отсортировать все числа от нуля до одного миллиарда. Идеальный оракул с нулевыми накладными расходами можно построить, просто используя значение элемента в качестве прогноза позиции. 1456? Это будет идти в позиции 1456…

И что же произошло, когда авторы попытались отсортировать числа, используя этот идеальный оракул с нулевыми накладными расходами?

К нашему удивлению, в этом микроэксперименте мы заметили, что время, необходимое для того, чтобы распределить ключи в их конечное отсортированное положение, несмотря на нулевую функцию oracle, заняло 38,7 секунды, а RadixSort-37,5 секунды.

Почему? Если вы ищете высокую производительность, вы не можете игнорировать механическую симпатию. Radix Sort тщательно разработан, чтобы эффективно использовать кэш L2 и последовательные обращения к памяти, в то время как Learned Sort делает произвольные обращения по всему целевому массиву.

Сочувствие к машине

Как можно адаптировать наученную сортировку, чтобы сделать ее эффективной для кэша? Решение состоит в том, чтобы изменить первый проход Изученной сортировки на каскадную сортировку ведра. Вместо определения конечной позиции в целевом массиве прогнозирование модели используется для определения того, в какую ячейку (или бин) должен входить элемент.

1. Пусть f - количество ведер (f для разветвления). Первая фаза усвоенной сортировки-это каскадная ведерная сортировка. Начальный проход использует предсказания модели для размещения входных элементов в один из упорядоченных сегментов f. Затем каждое из этих ведер разбивается на следующие f ведра и так далее рекурсивно, пока не будет достигнут пороговый размер ведра t. Если на каком-либо этапе прогноз модели помещает элемент в корзину, которая уже заполнена, этот элемент просто перемещается в корзину разлива.

2. Как только мы опустимся до размеров ведер t каждый из них приблизительно сортируется с использованием предсказаний модели для размещения элементов в точном предсказанном положении внутри ведра.

3. Объедините отсортированные ведра по порядку (некоторые могут иметь меньше t элементы в них), и используйте Сортировку вставки, чтобы исправить любые расхождения в порядке.

4. Сортировка и слияние разливного ведра.

   

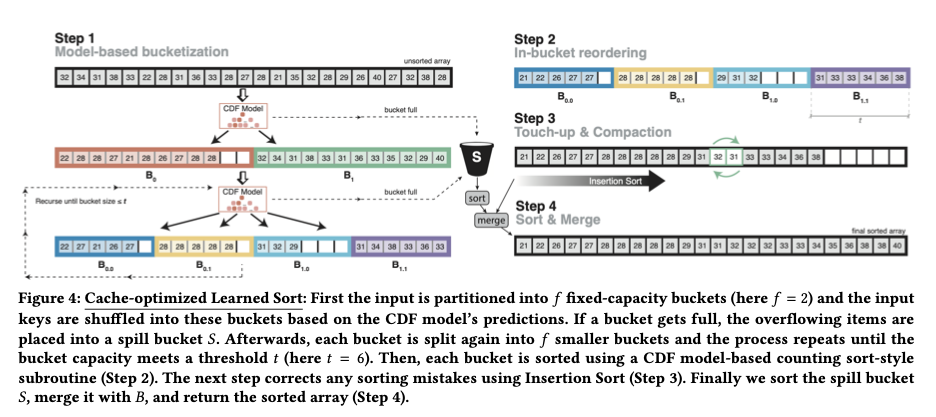
   Секрет хорошей работы с изученной сортировкой заключается в выборе f и t таким образом, по крайней мере одна строка кэша на ведро помещается в кэш, что делает шаблоны доступа к памяти более последовательными. Компромисс в настройке f заключается в следующем: f позволяет нам в большей степени использовать прогностическую силу модели на каждом шаге, меньшем f увеличивает вероятность того, что мы сможем добавить данные в заданное ведро, не вызывая промаха кэша. Для лучшей производительности, f должно быть установлено так, чтобы все горячие ячейки памяти помещались в кэш L2. Для оценочной установки это означало f было около 1000.

   Параметр t влияет на количество элементов, которые могут оказаться в разливном ведре. Эмпирическим путем авторы обнаружили, что максимальная производительность получается, когда менее 5% элементов попадают в ведро разлива, что приравнивается к t около 100 для больших наборов данных (см. §3.1.2).

   При наличии этих изменений, если количество сортируемых элементов близко к размеру ключевого домена (например, сортировка 232 элементы с 32-битными ключами), то Выученная сортировка выполняет почти идентично сортировке Radix. Но когда количество элементов намного меньше размера ключевого домена, сортировка Learne может значительно превзойти Сортировку Radix.

Ах да – о модели!

Все это, конечно, зависит от возможности обучить достаточно точную модель, которая может делать достаточно быстрые прогнозы, так что общее время выполнения для изученной сортировки, включая время обучения, все еще превосходит сортировку по Радиусу. Для этого авторы используют архитектуру Индекса рекурсивной модели (RMI), впервые представленную в "Случае для изученных индексных структур". Короче говоря, RMI использует слои простых линейных моделей, расположенных в иерархии, немного похожей на смесь экспертов.

Во время вывода каждый слой модели принимает ключ в качестве входных данных и линейно преобразует его для получения значения, которое используется в качестве индекса для выбора модели в следующем слое.

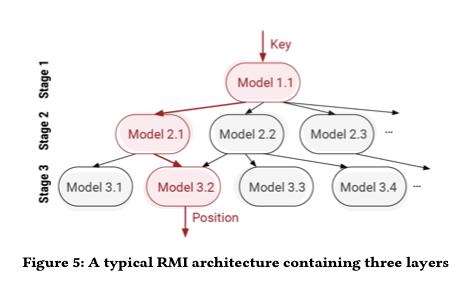
Основным новшеством, которое авторы вводят здесь, является использование линейной сплайн-подгонки для обучения (в отличие, например, от линейной регрессии с функцией потерь MSE). Сплайн-фитинг дешевле вычисляется и дает лучшую монотонность (сокращая время, затрачиваемое на фазу сортировки вставки). Каждая отдельная сплайн-модель подходит хуже, чем ее аналог линейной регрессии в замкнутой форме, но иерархия компенсирует это. Линейные сплайны приводят к более быстрому обучению в 2,7 раза и до 35% меньшему количеству свопов ключей во время сортировки вставок.

Оценка

На синтетических наборах данных, содержащих ключи двойной точности, следующие стандартному нормальному распределению, авторы сравнивали Изученную сортировку с различными оптимизированными для кэша и высоко настроенными реализациями альтернативных алгоритмов сортировки на языке C++, представляя наиболее конкурентоспособные альтернативы в своих результатах. На следующей диаграмме показаны скорости сортировки по входным наборам данных размером от одного миллиона до одного миллиарда элементов

Изученная сортировка превосходит альтернативу во всех размерах, но преимущество становится наиболее значительным, когда данные больше не помещаются в кэш L3 – пропускная способность в среднем на 30% выше, чем у следующего лучшего алгоритма.

Результаты показывают, что наш подход дает в среднем 3,38 - кратное улучшение производительности по сравнению с сортировкой C++ STL, которая является оптимизированным гибридом быстрой сортировки, 1,49 - кратное улучшение по сравнению с последовательной сортировкой по радиксу и 5,54-кратное улучшение по сравнению с реализацией на C++ Tim-сортировки, которая является функцией сортировки по умолчанию для Java и Python.

Преимущество изученной сортировки сохраняется и перед реальными наборами данных (§6.1 для наборов данных, включенных в тест), а также для различных типов элементов:

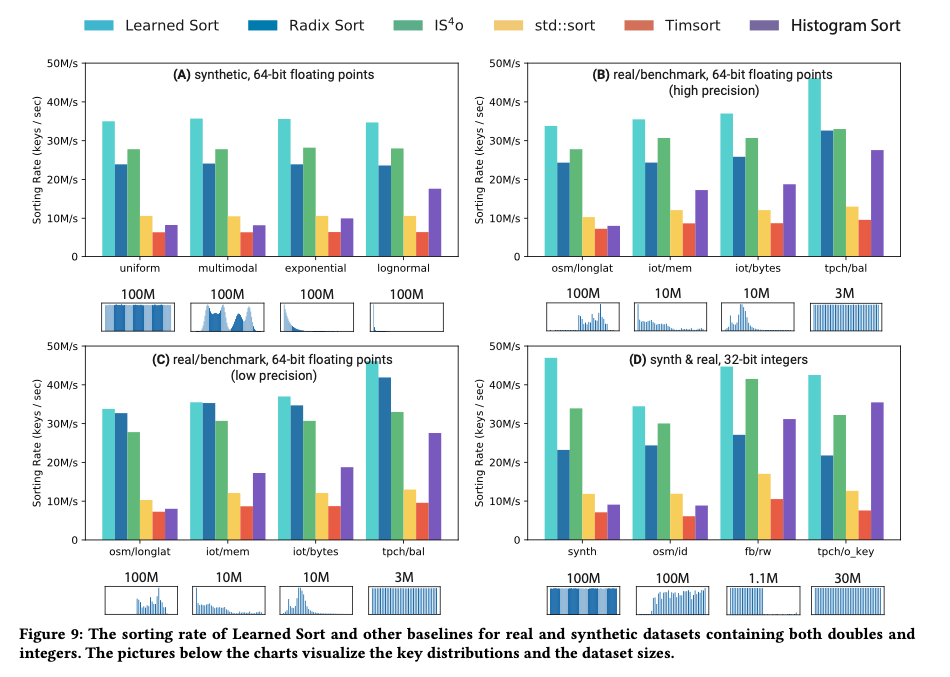
[Learned Sort] приводит к значительному повышению производительности по сравнению с наиболее конкурентоспособными и широко используемыми алгоритмами сортировки и знаменует собой важный шаг в построении алгоритмов и структур данных, улучшенных ML.

Расширения

В статье также описывается несколько расширений Изученной сортировки, включая сортировку на месте, сортировку по другим ключевым типам (изначально строкам) и повышение производительности для наборов данных с большим количеством повторяющихся элементов.